Area of triangle proof

There are many formulae for the area of triangle, in this article we would like to prove the following formula of area of triangle. which is more commonly used in mathematics.

$1)\Delta = \frac{1}{2} base * height$ where base is one side of the triangle and height is the altitude on the considered side from the opposite vertex.

1) Proof of $\Delta\ = 1/2\ base * height$

Proof:

Let’s prove the formula using normal geometry. For that let’s consider a paralellogram ABCD as shown in the figure. As we can see in the diagram there is a triangle ABC in paralelllogram ABCD. since $\triangle ABC$ and $\triangle CDA$ have equal lenghts of sides both the triangles, that means both triangles are congruent, which means areas of $\triangle ABC$ and $\triangle CDA$ must be equal. that means area of paralellogram is twice the area of $\triangle ABC$ or $\triangle ADC$.

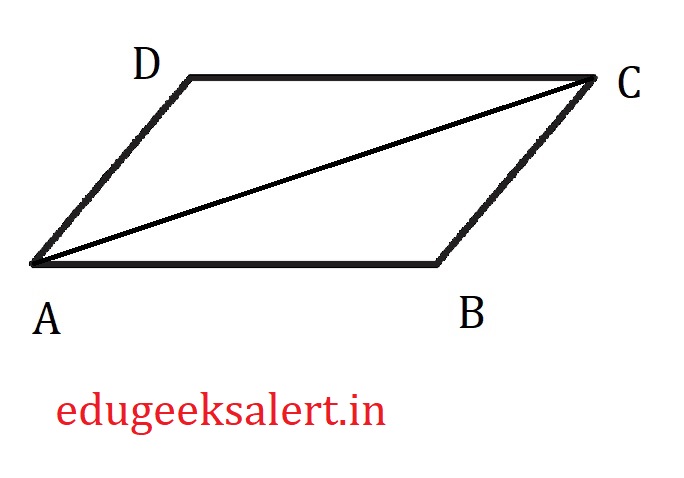
therefore area of $\triangle$ ABC = $\frac{1}{2}$ area of ABCD

Let’s not use the area of paralellogram formula blindly instead let’s understand how that formula is built. In order to find the area of paralellogram let’s draw DE and CF line segments perpendicular the side AB as shown below.

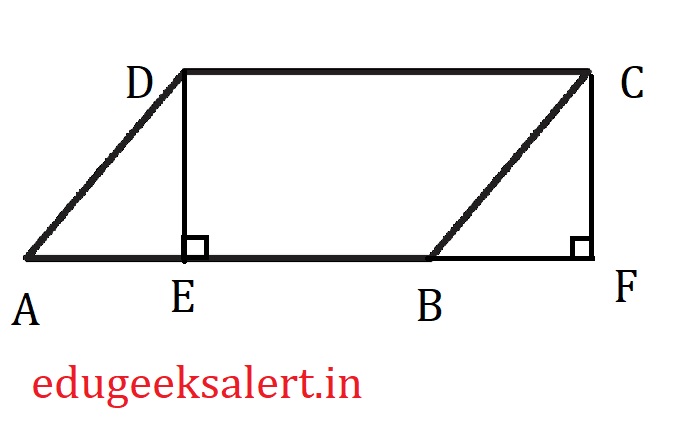
Now look at the diagram we have produced two triangles $\triangle$ ADE and $\triangle$ BCF, let’s prove that these two triangles are congruent.

$$In\ \triangle\ ADE\ and\ \triangle\ BCF$$

since AD and BC are opposite sides of paralellogram $$AD=BC$$

since AD $\parallel$ BC and AF is transversal corresponding angles must be equal, $$\angle DAE= \angle CBF$$

since $\angle DEA$= $\angle CFB$= $90^0$ and $\angle DAE= \angle CBF$ then $$\angle ADE=\angle BCF$$

by Angle Side Angle axiom $\triangle ADE$ and $\triangle BCF$ are congruent. By this we can say that:

$$area\ of\ paralellogram\ ABCD = area\ of\ rectangle\ EFCD$$

therefore, $$area\ of\ paralellogram\ ABCD = length * breadth$$

from the diagram we can understand that length of rectangle EFCD is base of $\Delta$ ABC and breadth of rectangle EFCD is altitude(height) of $\Delta$ ABC

therefore area of triangle ABC = $\frac{1}{2}$ area of paralellogram ABCD = $\frac{1}{2} base * height$