Sine rule or Laws of sine

Statement: In a $\triangle$ ABC with a, b and c are the lengths of sides BC, CA and AB respectively then

$$\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}= 2R$$

Where R is the circum radius of the $\triangle$ ABC.

Therefore, $$a= 2R\ Sin\ A, b= 2R\ sin\ B, c= 2R\ sin\ C$$

Proof: Let’s consider the $\triangle$ ABC as shown in the figure circumscribed. O is the circum centre.

We know that a, b and c are lengths of sides of $\triangle$ ABC and R is the circum radius.

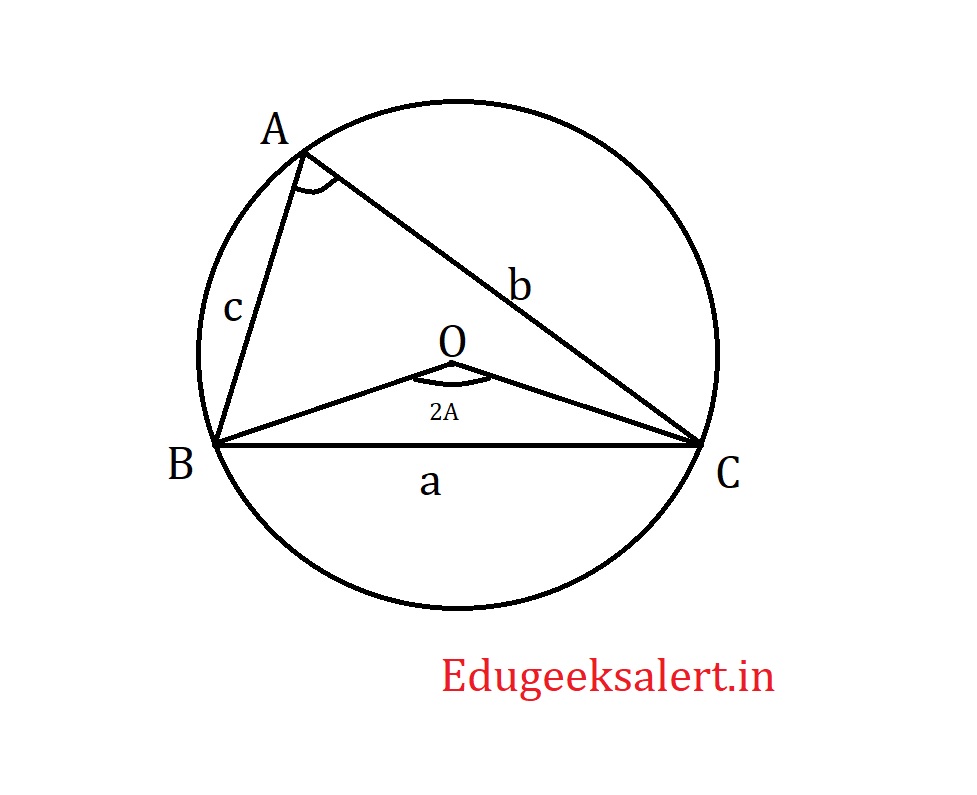
From the diagram we can see that BC is the chord of the circle. From circle properties we know that

$$\angle BOC = 2A$$

Let’s draw altitude to OM in $\triangle$OBC perpendicular to side BC. As OB and OC are also radii of the circle we can understand that $\triangle$OBC is an isosceles triangle. In an isosceles triangle altitude and median coincides. Therefore OM is not just altitude but also median. Therefore BM =$\frac{a}{2}$

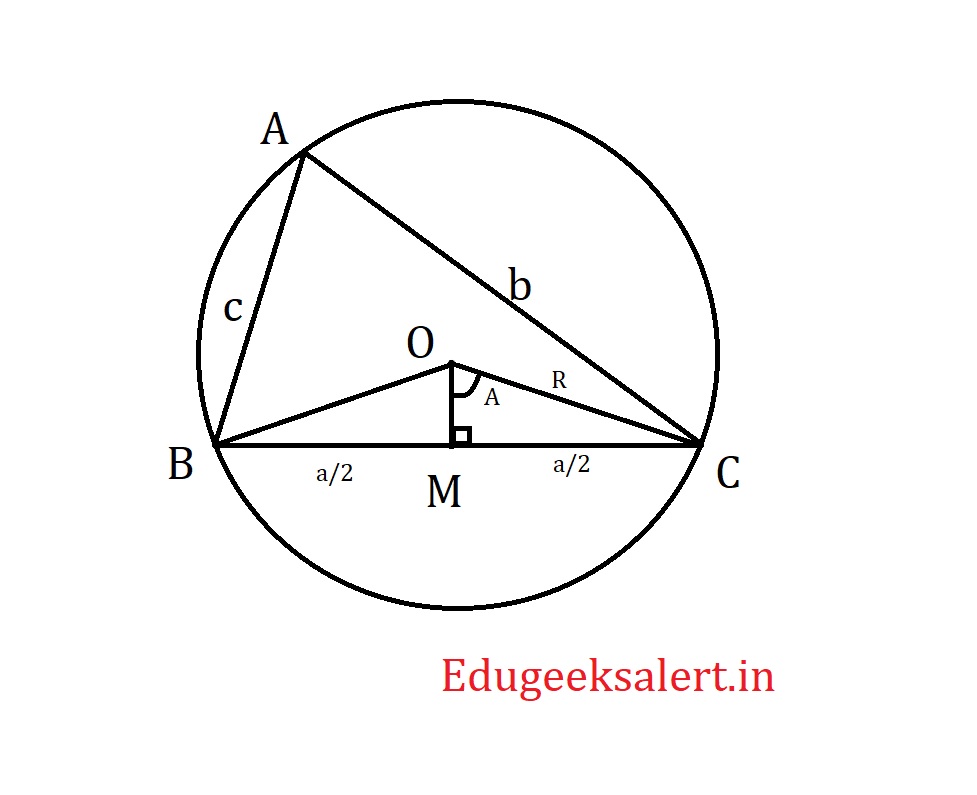
Now let’s consider $\triangle$ OMB, since OBC is isosceles OM bisects $\angle$ BOC. And $\angle$ OMB =$90^0$

$$sin \ \angle BOM = \frac{MB}{OB}$$

$$sin \ A= \frac{a}{2R}$$

$$a=2R\ sin\ A$$

Similarly we can prove that c = 2R sin C and b= 2R sin B.

And we can write

$$\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}= 2R$$