Proof of Pythagoras theorem

(There are thousands of independent ways of proving the pythagoras theorem. It was discovered by many mathematicians before and after pythagoras independently. where as proofs are done in various methods. People are so fascinated about this theorem becasue it is so important theorem, because it is useful in almost every subject directly or indirectly)

In this article we used one method to prove the theorem. hope yu find it intresting.

Statement: square of length hypotenuse of a right angled triangle is equal to the sum of squares of lengths other two sides

$$c^2 = a^2+b^2$$

Where c is the length of hypotenuse of a right angled triangle, while a and b are lengths of other two sides

Proof:

Consider the triangle ABC where $\angle$ B = $90^0$ as shown in the figure. Let’s draw BD line segment such that BD is perpendicular to side AC creating two right angled triangles BDA and BDC

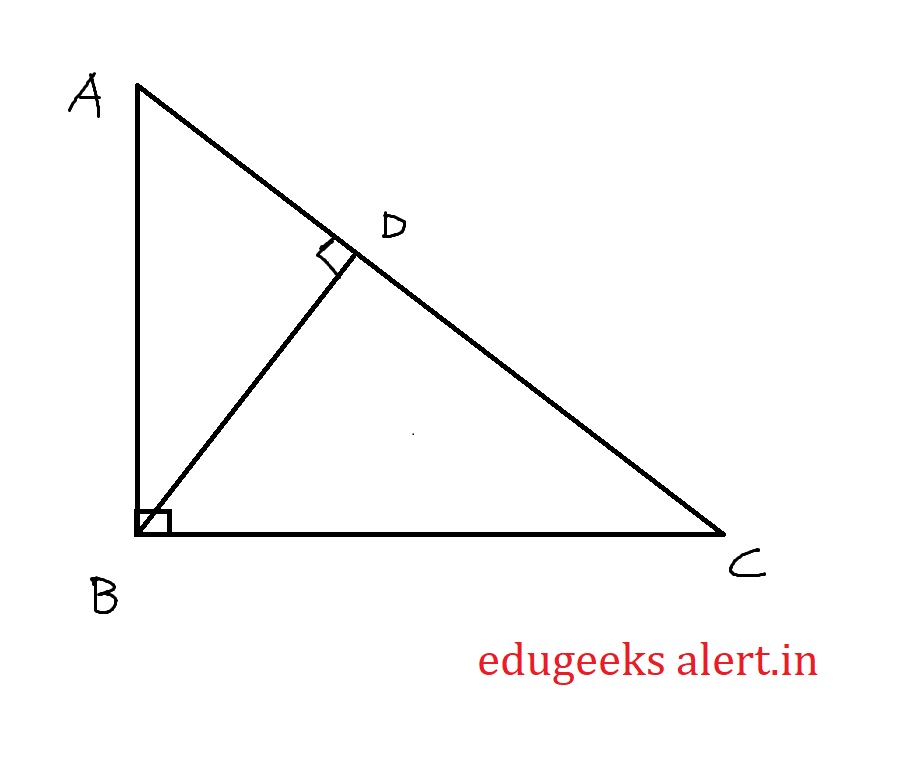
$$Let’s\ compare\ \triangle ABC\ with\ \triangle\ ABD$$

$$\angle BAC = \angle BAD$$

$$\angle ABC = \angle ADB = 90^0$$

Therefore by Angle-Angle axiom we can say that $\triangle$ ABC $\sim$ $\triangle$ ADB

$$\triangle ABC \sim \triangle ADB$$

$$\frac{AB}{AD}=\frac{AC}{AB}$$

$$AB^2 = AC AD ————(1)$$

Let’s compare \triangle ABC with $\triangle$ BDC

$$\angle BCA = \angle BCD$$

$$\angle ABC = \angle BDC = 90^0$$

Therefore by Angle-Angle axiom we can say that $\triangle$ ABC $\sim$ $\triangle$ BDC

$$\triangle ABC \sim \triangle BDC$$

$$\frac{BC}{DC}=\frac{AC}{BC}$$

$$BC^2 = DC AC ————(2)$$

From (1) and (2), Add (1) and (2)

$$AB^2 + BC^2 = AC AD + DC AC$$

$$AB^2 + BC^2 = AC ( AD + AC)$$

From the diagram we can see that AC = AD + AC

$$AB ^2 + BC^2 = AC ^2$$

Hence proved that in a right angled triangle square of length of hypotenuse is equal to the sum of squares of the lengths of other two sides.