This is the multi-page printable view of this section. Click here to print.
Trigonometric Properties of triangle
1 - cos rules or Laws of cos
Cos rule or law of cos states that in A $\triangle$ ABC a, b and c are lengths of sides BC CA and AB. Then
$$a^2=b^2+c^2-2bc \ Cos \ A$$
$$b^2=a^2+c^2-2ac\ Cos\ B$$
$$c^2=a^2+b^2-2ab\ Cos\ C$$
$$Or$$
$$cos\ B= \frac{a^2+c^2-b^2}{2ac}$$
$$cos\ C= \frac{b^2+a^2-c^2}{2ba}$$
$$cos\ A= \frac{b^2+c^2-a^2}{2bc}$$
It seems like a different form of Pythagoras theorem for every triangle doesn’t it?
Proof:
Let’s consider a $\triangle$ ABC as shown in the figure with a, b and c being the lengths of the sides BC, CA and AB. we can represent the triangle vectorically as shown in the diagram. That means $\vec{AB}$, $\vec{BC}$ and $\vec{AC}$ are forming the triangle so we can understand that | $\vec{AB}$ | = c, | $\vec{BC}$ | = a and | $\vec{AC}$ | = b.
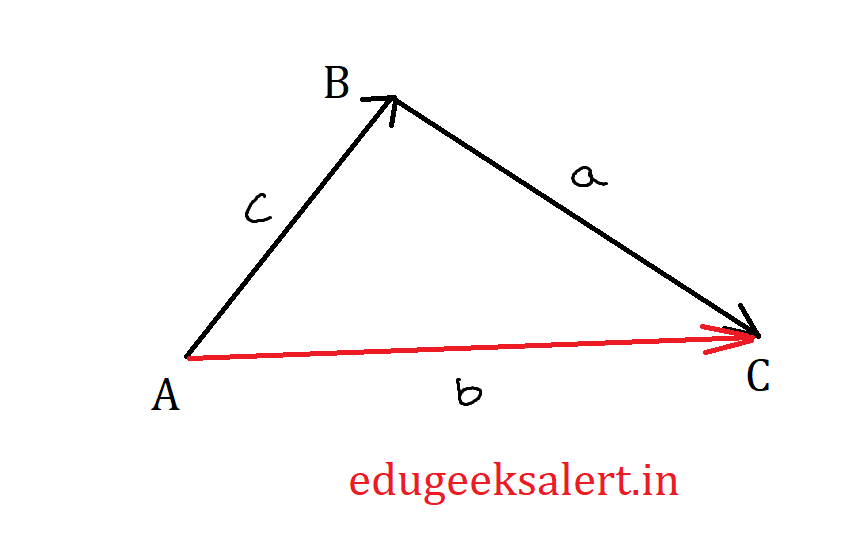
From the triangle we can write that
$$\vec{AC}=\vec{AB}+\vec{BC}$$
Apply mod on both sides
$$| \vec{AC} |=| \vec{AB} + \vec{BC} |$$
$$ b = | \vec{AB} + \vec{BC} |$$
From vectors we have $| \vec{x} + \vec{y} | = \sqrt {x^2+y^2+2xy\ cos(\vec{x},\vec{y})}$
To find the angle between $\vec{AB}$ and $\vec{BC}$ lets extend the $\vec{AB}$ so that both vector tails meet. Let $\alpha$ be the angle between those two vectors.
(note: we extended the vector to find the angle between two vectors by not considering B as angle, because angle between two vectors is angle made by vectors when both heads meet or tails meet but not one tail and one head)
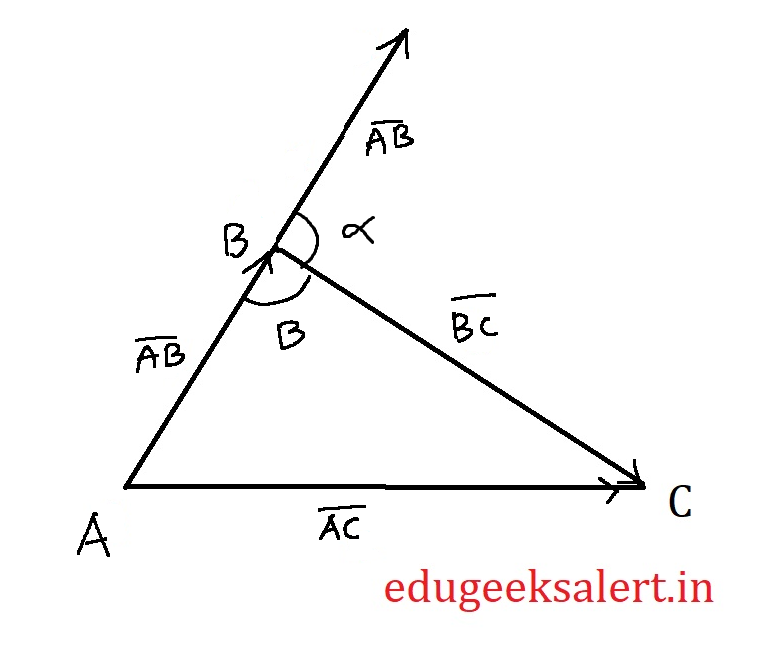
From the above figure we can find $\alpha$
$$\alpha + B=180^0$$
$$\alpha =180^0 - B $$
Therefore,
$$ b = | \vec{AB} + \vec{BC} |$$
$$ b =\sqrt{ | \vec{AB}|^2 +| \vec{BC} |^2 +2 | \vec{AB} | |\vec{BC}| cos(\vec{AB} , \vec{BC})}$$
$$ b =\sqrt{ c^2 + a^2 +2 ca\ cos(\alpha)}$$
$$ b =\sqrt{ c^2 + a^2 +2 ca\ cos(180^0 - B)}$$
$$ b =\sqrt{ c^2 + a^2 -2 ca\ cos\ B}$$
$$b^2=a^2+c^2-2ac\ Cos\ B$$
Hence proved.
Now we can extend this proof by simplification and we can write
$$cos\ B= \frac{a^2+c^2-b^2}{2ac}$$
Similarly we can do the same for the other two angles and we can prove the other two equations of cos rule
2 - Sine rule or Laws of sine
Statement: In a $\triangle$ ABC with a, b and c are the lengths of sides BC, CA and AB respectively then
$$\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}= 2R$$
Where R is the circum radius of the $\triangle$ ABC.
Therefore, $$a= 2R\ Sin\ A, b= 2R\ sin\ B, c= 2R\ sin\ C$$
Proof: Let’s consider the $\triangle$ ABC as shown in the figure circumscribed. O is the circum centre.
We know that a, b and c are lengths of sides of $\triangle$ ABC and R is the circum radius.
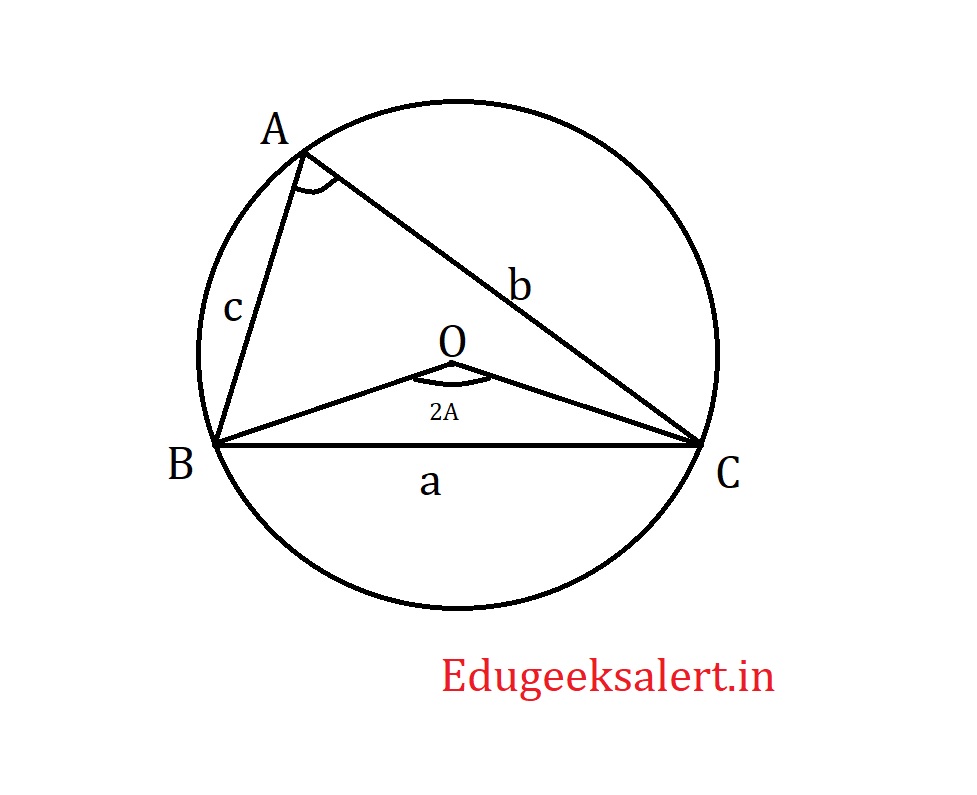
From the diagram we can see that BC is the chord of the circle. From circle properties we know that
$$\angle BOC = 2A$$
Let’s draw altitude to OM in $\triangle$OBC perpendicular to side BC. As OB and OC are also radii of the circle we can understand that $\triangle$OBC is an isosceles triangle. In an isosceles triangle altitude and median coincides. Therefore OM is not just altitude but also median. Therefore BM =$\frac{a}{2}$
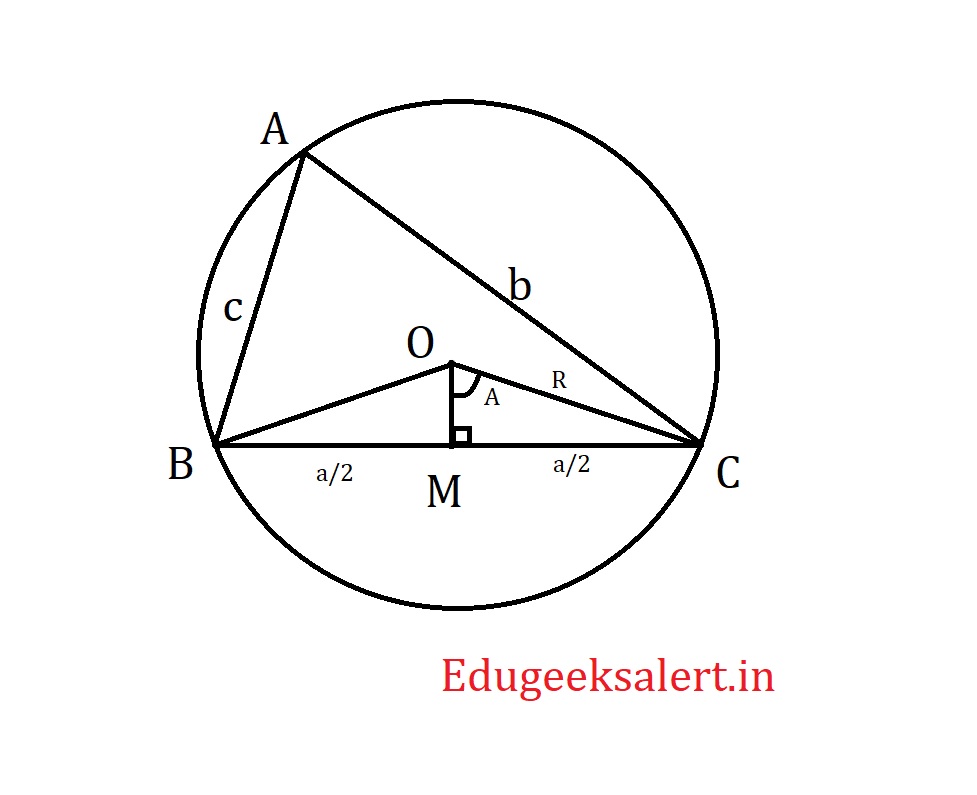
Now let’s consider $\triangle$ OMB, since OBC is isosceles OM bisects $\angle$ BOC. And $\angle$ OMB =$90^0$
$$sin \ \angle BOM = \frac{MB}{OB}$$
$$sin \ A= \frac{a}{2R}$$
$$a=2R\ sin\ A$$
Similarly we can prove that c = 2R sin C and b= 2R sin B.
And we can write
$$\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}= 2R$$