Maths

• 1: Factorial of 100
• 2: Logarithms
• 2.1: Definition and properties
• 2.2: Proofs of Logarithmic properties
• 2.3: Practice Problems on logarithms
• 3: progression
• 3.1: Arithmetic progression
• 3.2: Geometric progression
• 3.3: Relationship between Arithematic and Geometric Means
• 4: Proof of Pythagoras theorem
• 5: triangle
• 5.1: Area of triangle proof
• 6: Trigonometry
• 6.1: Trigonometric Identities
• 6.2: Trigonometric Identities (problem solving)
• 6.3: Trigonometric ratios of multiple of Angle-2A
• 6.4: Trigonometric ratios of multiple of Angle-3A
• 6.5:
• 6.6: Trigonometric transformations from sum( or difference) to product and vice-versa
• 7: Trigonometric Properties of triangle
• 7.1: cos rules or Laws of cos
• 7.2: Sine rule or Laws of sine

1 - Factorial of 100

Factorial of hundred:

The factorial of a positive integer n is the product of all the positive integers from 1 to n. For example, the factorial of 4 is 4! = 4 * 3 * 2 * 1 = 24. The factorial of 100 is 100! = 100 * 99 * 98 * … * 2 * 1. This is a very large number, equal to approximately 9.3 x 10^157. It has 158 digits! Here is the first few digits of 100!:

eg: $4! = 4 \times 3 \times 2\times 1 = 24$

100!

$100! = 100 \times 99 \times 98 \times 97 \times …….. 4 \times 3 \times 2\times 1 $ = $93326215443944152681699238856266700490715968264381621468592963895217599993229915$ $608941463976156518286253697920827223758251185210916864000000000000000000000000$

The factorial of a positive integer n is the product of all the positive integers from 1 to n. For example, the factorial of 4 is 4! = 4 * 3 * 2 * 1 = 24. The factorial of 100 is 100! = 100 * 99 * 98 * … * 2 * 1. This is a very large number, equal to approximately 9.3 x 10^157. It has 158 digits! Here is the first few digits of 100!:

Factorial of 0! = 1 Proof

The factorial of 0, written as 0!, is defined to be equal to 1. This may seem counterintuitive at first, but there are a few different ways to justify this definition.

One way to think about it is to consider the factorial function as a way of counting the number of ways to arrange a certain number of objects. For example, if you have 3 objects, there are 3! = 6 ways to arrange them: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). If you have no objects, there is only 1 way to arrange them: the empty set, or “nothing.”

Another way to justify the definition of 0! as 1 is to consider the definition of the factorial function as a product of all the positive integers from 1 to n. When n = 0, there are no positive integers to include in the product, so the product is equal to 1.

It is also possible to define 0! as the limiting value of n! as n approaches 0. This can be shown using mathematical techniques, such as L’Hopital’s rule. However, this definition relies on advanced mathematical concepts and may not be as intuitive as the other explanations.

2 - Logarithms

2.1 - Definition and properties

Logarithm: For a number and base, the power the base should have so that it is equal to the given number is called a logarithm.For example, the logarithm of 8 with base 2 means what power should 2 have so that it is equal to 8. 2³=8, the answer is 3.

logarithm is represented as log_b a where a and b are non-zero positive numbers.

Where a is the number inside the logarithmic function and b is the base. And we read it as log a base b.

Symbolically the above example can be represented as: Log₂ 8 =3

I) find the values for the following logarithms:

1. log₃ 27
2. log₁₀ 100
3. log₄ 2
4. log₁₀ (0.1)

Solutions are at the end of the article.

Logarithm in fact is an inverse of exponential function. Let’s see how logarithm and exponents are interconvertible:

a^b=x ------> b= log_a x

Look at the example 2³=8, this is represented as log₂ 8=3

This is how we interconvert exponents into logarithms and vice versa.

II) convert the following logarithms into exponents

1. log_a b = x
2. log₂₅ 5= 1/2
3. log₃ 9= 2

Solutions are at the end of the article.

Properties:

For a, b, x, y being postive non-zero numbers.

Product rule: Log_a xy = log_a x+ log_a y

Quotient rule: Log_a $\frac{x}{y}$ = log_a x- log_a y

Power rule: (i) log_b $a^m$ = m log_b a

Power rule: (ii) log_bⁿ a= $\frac{1}{n}$ log_b a

log_b a= $\frac{1}{log_a b}$

log_b a= $\frac{log_x a}{log_x b}$

log_a 1 = 0

Other properties:

log_a a= 1

If log_b a= log_b c then a=c

log_b $\frac{1}{a}$=log_{$\frac{1}{b}$} a= -log_a a

a^{log_a x} = x

log_a 0 is undefined

III) Solve the following logarithms:

1. log₅ x = log₅ 2 + log₅ 7
2. log_b x+log_b 1/x
3. log₅ 15 - log₅ 3
4. log₅ 125
5. log₁₆ 4

Solutions are at the end of the article.

Sometimes we drop bases in logarithms for base 10 and natural logarithms. Log₁₀ a can be represented dropping 10 i.e. log a. And logarithm with natural base ’e’ can be represented as ln x (=log_e x)

Solutions:

I

1) ans=3

Sol: log₃ 27 = log₃ $3^3$

Using the property $log_b$ $a^n$ = n $log_b$ a

= 3log₃ 3

Using the property log_a a=1

= 3

2) ans=2

Sol:

log₁₀ 100 = log₁₀ $10^2$

Using the property log_b $a^n$ = n log_b a

= 2log₁₀ 10

Using the property log_a a=1

=2

3) ans=½

Sol:

log₄ 2 = log_2² 2

Using the property log_bⁿ a = $\frac{1}{n}$ log_b a

= $\frac{1}{2}$ log₂ 2

Using the property log_a a=1

= $\frac{1}{2}$

4) ans=-1

Sol:

Log₁₀ (0.1) = log₁₀ $\frac{1}{10}$

Using the property Log_a $\frac{x}{y}$ =log_a x- log_a y

= - log₁₀ 10

Using the property log_a a=1 =-1

II)

1. $a^x$
2. 5= 25^{$\frac{1}{2}$}
3. 9= $3^2$

III)

1) x=14

Sol:

log₅ x = log₅ 2 + log₅ 7

Using the property Log_a xy=log_a x+ log_a y

log₅ x = log₅ 2*7

Using the property if log_a b=log_a c then b=c

x=14

2) ans=0

Sol:

log_b x+log_b 1/x

Using the property Log_a xy =log_a x+ log_a y

=log_b x* $\frac{1}{x}$

=log_b 1

Using the property Log_a 1 = 0

=0

3) ans= 0

Sol:

log₅ 15 - log₅ 3

Using the property Log_a $\frac{x}{y}$ =log_a x- log_a y

=Log₅ $\frac{15}{3}$

= log₅ 5

Using the property Log_a 1 = 0

=0

4) ans =3

Sol:

log₅ 125

=log₅ $5^3$

Using the property log_b aⁿ = n log_b a

=3 log₅ 5

Using the property log_a a=1

=3

5) ans =½

Sol:

log₁₆ 4

=log_4² 4

Using the property log_bⁿ a = $\frac{1}{n}$ log_b a

=½ log₄ 4

Using the property log_a a=1

=½

2.2 - Proofs of Logarithmic properties

1) Product Rule: Log_a xy = log_a x+ log_a y

proof:

let log_a x = m, log_a y = n

convert these logarithms into exponents

x=a^m and y=aⁿ

multiply the above equations

xy=a^m * aⁿ

Using the property b^p * b^q=b^p+q from exponents we can write the above equation as follows

xy=a^m+n

Convert back into logarithm

log_a xy = m+n

on substituting the values m= log_a x and n =log_a y we get

log_a xy = log_a x + log_a y

2) Quotient Rule: Log_a $\frac{x}{y}$ =log_a x- log_a y

proof:

let log_a x = m, log_a y = n

convert these logarithms into exponents

x=a^m and y=aⁿ

divide the above equations

$\frac{x}{y}$ = $\frac{a^m}{a^n}$

using the property b^p/b^q=b^p-q from exponents we can write the above equation as follows

$\frac{x}{y}$=a^m-n

convert into logarithm

log_a $\frac{x}{y}$=m-n

on substituting the m= log_a x & n =log_a y we get

log_a (xy)=log_a x - log_a y

3) Power Rules:

i) log_b $a^m$ = m log_b a

Proof:

let x=log_b a

convert logarithm into exponent

b^x=a

taking both sides of the equation to m’th power

(b^x)^m=a^m

using the property (a^m)ⁿ=a^mn from exponents we can write the above equation as follows

b^xm=a^m

convert back to logarithm

xm=log_b a^m

substitute x=log_b a back in the equation and interchanging

log_b a^m = m log_b a

ii) log_bⁿ a= $\frac{1}{n}$ log_b a

proof:

let log_bⁿ a=x

convert this into exponential form

a=(bⁿ)^x

use exponential property

(a^m)ⁿ=a^mn=(aⁿ)^m

a=(b^x)ⁿ

use the property if a^m=b then a=b^{$\frac{1}{m}$} from exponents we can write the above equation as follows

a^{$\frac{1}{n}$}=b^x

interchanging and converting into logarithmic form

b^x=a^{$\frac{1}{n}$}

x=log^b a^{$\frac{1}{n}$}

substitute the value of x=log_bⁿ a and use logarithmic property log_b a^m= m log_b a

log_bⁿ a= $\frac{1}{n}$ log_b a

4) log of 1 rule: log_b 1=0

Proof:

from exponents we have:

b⁰=1

convert this into logarithmic form

0=_b 1

5) Change of Base Rule: log_b a= $\frac{log_x a}{log_x b}$

Proof:

let log_x a=p, log_x b=q

Convert these logarithms into exponential forms

a=x^p and b=x^q

Substituting in the Left hand side of the to solve into right hand side of the Rule

L.H.S. : log_b a= log_xⁿ x^m

Using the power rule: log_n^q a^p= $\frac{p}{q}$ $log_b$ a

log_b a= $\frac{p}{q}$ log_x x

Using the Rule log_a a=1

Log_b a= $\frac{p}{q}$

Substituting the assumed p= $log_x$ a, q= $log_x$ b

Log_b a= $\frac{log_x a}{log_x b}$

6) log_b $\frac{1}{a}$ =log_{$\frac{1}{b}$} a= -log_b a

Proof:

i) Log_b (1/a)=log_b a^-1

Using the property log_a b^m=m log_a b =-log_b a

ii) log_{$\frac{1}{b}$} a=log_$b^{-1}$ a

log_b $\frac{1}{a}$ =log_{$\frac{1}{b}$} a= -log_b a

7) a^{log_a x} = x

Proof:

Let p=a^{log_a x}

Converting the above exponent into logarithm

Log_a p = log_a x

Using he property if log_b a= log_b c then a=c

p=x

But we assumed p=a^{log_a x}

Therefore a^{log_a x} = x

2.3 - Practice Problems on logarithms

I) write the following in the logarithmic format

1. $5^3$ = 125

2. $2^4$ = 16

3. $4^{-2}=\frac{1}{16}$

4. $(\frac{1}{2})^{-3}=8$

5. $\sqrt {81}$ = 9

6. $x^{2a}=y$

II) convert the following logarithms into exponents

1. x= $log_3\ y$

2. $log_x\ 1$ =0

3. ln x = 5

4. $log\ 100=2$

5. $log_8\ 2=\frac{1}{3}$

III) Find the values of x

1. $log_5\ 25$ = x

2. $log_{100}\ 1000$ = x

3. $log_{23}\ 1$ = x

4. $log_3\ \frac{1}{27}$ = x

5. $log_x\ 49$ = 7

6. $log_9\ x$ = -3

7. $log_5\ \frac{1}{5}$ = x

8. $log_8\ x=1- \frac{1}{2}$

9. $log_{12}\ 1$ = x

10. $log_{32}\ 2$ = x

11. $log_4\ \frac{1}{32}$ = x

12. $log_{12}\ \frac{1}{144}$ = x

IV) Write the following expressions in terms of logs of x, y and z

1. log $x^3y$

2. log $xyz$

3. log $\sqrt[3]x y^2 z$

4. log $\frac{x}{z^3}y$

5. log $\sqrt[5]{x^3yz^2}$

6. log $x \sqrt{ \frac{\sqrt{x^3y^2}}{z^4}}$

7. log $(x^3y)^{\frac{1}{2}}$

8. log $\frac{x^3}{y}$

V) Solve the following logarithmic equations

1. ln x =-2

2. log (7x+2) = 2

3. log x + log (x+1) = log 4x

4. 2log x = log 2 + log(3x-4)

5. $log_3\ (x+3) + log_3\ (x+2) - log_3\ 10 = log_3\ x$

6. $log_2\ x + log_2\ (x+3) = 1$

VI) If log 2= x, log 3 =y then express the following in x and y

1. log 24

2. log 225

3. log 150

4. $log_7\ 980$

5. log 343

6. log 12.5

7. log 0.2

8. log 15

9. log 2.5

10. $log_7\ 3.5$

VII) Solve the following equations

1. $3^x$ - 1 =8
2. $2^{2x}-2^x-6$=0
3. $3^{1-x}=5^x$
4. $3^{2x-1}+3{x+2}-18$=0
5. $e^{2x}-2e^{x}-15$=0

3 - progression

3.1 - Arithmetic progression

A progression in which the difference between any two consecutive terms his always as same fixed quantity, such a progression is called arithmetic progression or simply AP. And the fixed difference is called common difference.

If a is the first time and t is the common difference then general AP form is:

a, a+t, a+2t, a+3t ……..

Where we denote terms as follows:

$a_1$ = a

$a_2$ = a+t

$a_3$ = a+ 2t and so on.

General term $a_n$ = a+(n-1)t . That is $a_n$ is the $n^th$ term with a being the first term and t is the common difference.

Examples of AP

1. 1,2,3,4,5,6,7……..

2. 1,3,5,7,9….

3. 9,6,3,0,-3….

4. 1,11,21,31,….

Sum of first n terms of AP

statment: Let $S_n$ be the sum of first n terms of AP $a_1,a_2,a_3,…….a_n$ then $S_n$ = $\frac{n}{2}[2a+(n-1)t]$ = $\frac{n}{2}[a_1+a_n]$

Proof:

Given the AP, $a_1,a_2,a_3,…….a_n$

$$S_n = a_1 + a_2 + a_3 + …… + a_n$$

$$S_n = a + (a+t) + (a+2t) + ….. + [a+ (n-1)t]$$

$$S_n = \sum_{r=1}^n[a+(n-1)t]$$

$$S_n=\sum_{r=1}^{n} a + \sum_{r=1}^{n}(n-1)t $$

As a and t are constants we can take them out of summation

$$S_n = a \sum_{r=1}^{n} 1 + t \sum_{r=1}^{n} (n-1)$$

$$Here \sum_{r=1}^{n} 1 = n \ because\ 1\ is\ added\ n\ times$$

$$S_n = a n + t [\sum_{r=1}^{n} n - \sum_{r=1}^{n} 1]$$

$$And\ we\ know\ that\ sum\ of\ first\ n\ natural\ numbers\ i.e. \sum_{r=1}^{n} n = \frac{n(n+1)}{2}$$

$$S_n = a n + t [ \frac{n(n+1)}{2} - n]$$

$$S_n = n [ a + t (\frac{(n+1)}{2} -1)]$$

$$S_n = n [ a + t \frac{(n-1)}{2} ]$$

$$S_n = \frac{n}{2} [ 2a + t (n-1)]$$

Points to be noted

1. If every term in an AP is multiplied by a constant k then new series will also be in AP with common difference kt
2. If every term in an AP is added with k then the new series will be in AP with common difference (k+t)

Arithmetic Mean (AM)

Definition: If $a_1, a_2, a_3, …..a_n$ are real numbers then $\frac{a_1 + a_2 + a_3 + ….. + a_n}{n}$ is called arithmetic mean of $a_1, a_2, a_3, …..a_n$.

In such AM we can observe something interesting. AM of any two numbers make another AP

i.e. if A is the AM of a and b then a, A, b are in AP

If b is the AM of a and c then a, b, c are in AP

Proof:

Given b is the arithematic mean of a and c that means

b = $\frac{a+c}{2}$

for a, b ,c to be in AP the difference between adjacent terms must be equal i.e.

b-a = c - b

as b = $\frac{a+c}{2}$

b-a = $\frac{a+c}{2}$ - a = $\frac{c-a}{2}$

and c-b = c - $\frac{a+c}{2}$ = $\frac{c-a}{2}$

we got b-a = c-b

therefore a,b,c are in AP.

3.2 - Geometric progression

Statement: A progression in which the ratio of two consecutive terms is always same constant, such a progression is called geometric progression or simply called GP. and the constant ratio is called common ratio

i.e. if $a_1,a_2,a_3,…….a_n$ are in GP then

$$\frac{a_2}{a_1}=\frac{a_3}{a_2}=\frac{a_4}{a_3}=\frac{a_5}{a_4}=………$$

General form of GP is $a, ar, ar^2, ar^3, ar^4 ……….$ where

first term is $a_1=a$

second term is $a_2=ar$

third term is $a_3=ar^2$ ……..

$n^{th}$ term is $a_n=ar^{n-1}$

Sum of n terms of a GP

Statement:

1. sum of first n terms of a geometric progression is $S_n= \frac{a(r^n-1)}{r-1}$ when r $\neq$ 1
2. if r=1 then $S_n$ = a + a + a + a + a + a +. . . . (n terms) = na
3. if |r|<1 and n = $\infty$ then $S_n = \frac{a}{1-r}$

Proof: Case-1)

$S_n= a+ar+ar^2+…..+ar^{n-1}$—-(1)

now multiply common ration r on both sides of the equation

$rS_n =ar+ar^2+ar^3+……+ar^n$—–(2)

let’s subtract equation (1) from equation (2)

$S_n = a+ar+ar^2+…..+ar^{n-1}$

$\underline{- rS_n = -(ar+ar^2+ar^3+……+ar^n) } $

$(1- r) S_n= [a- ar^n]$

$S_n= \frac{a(1- r^n)}{1-r}$

Case-3)

given |r|<1 and n = $\infty$

from the above proof we can write

$$ S_n= \frac{a(1- r^n)}{1-r}$$

as |r|<1 and n = $\infty$ then $r^n = 0$

$$ S_n= \frac{a(1- 0)}{1-r}$$

$$ S_n= \frac{a}{1-r}$$

Geometric mean (GM):

If $a_1,a_2,a_3,…….a_n$ are positive numbers then $(a_1a_2a_3…….a_n)^{1/n}$ is called geometric mean of $a_1,a_2,a_3,…….a_n$.

therefore GM of a and b is

$$GM=\sqrt{ab}$$

3.3 - Relationship between Arithematic and Geometric Means

Relation: For A being the arithematic mean and G being the Geometric mean of positive real numbers a and b then we habe A= $\frac{a+b}{2}$ and G= $\sqrt {ab}$ then $$A \geq G$$

Proof: Given two positive numbers a and b and A and G are arithematic and geometric means respectively.

$$A-G=\frac{a+b}{2}-\sqrt {ab}$$

$$A-G=\frac{a+b-2\sqrt {ab}}{2}$$

$$A-G=\frac{(\sqrt a)^2+(\sqrt b)^2-2\sqrt {ab}}{2}$$

using the algebraic formula $a^2+b^2-2ab=(a+b)^2$ in the equation

$$A-G=\frac{(\sqrt a-\sqrt b)^2}{2}$$

for two positive numbers a and b $(\sqrt a-\sqrt b)^2$ is always positve or zero, which can be represented as

$$A-G=\frac{(\sqrt a-\sqrt b)^2}{2} \geq 0$$

that implies

$$A \geq G$$

hence proved for two numbers

here $A = G$ would mean that a=b. that is for the same number both AM and GM will be same.

Similarly this can be extrapolated and can be expressed more generally as for $a_1, a_2, a_3, …..a_n$ where all being positive numbers then arithematic mean A = $\frac{a_1 + a_2 + a_3 + ….. + a_n}{n}$ and geometric mean $(a_1a_2a_3…….a_n)^{1/n}$. Then it can be shown that

$$A \geq G$$

and A=G when $a_1= a_2= a_3= …..=a_n$

4 - Proof of Pythagoras theorem

(There are thousands of independent ways of proving the pythagoras theorem. It was discovered by many mathematicians before and after pythagoras independently. where as proofs are done in various methods. People are so fascinated about this theorem becasue it is so important theorem, because it is useful in almost every subject directly or indirectly)

In this article we used one method to prove the theorem. hope yu find it intresting.

Statement: square of length hypotenuse of a right angled triangle is equal to the sum of squares of lengths other two sides

$$c^2 = a^2+b^2$$

Where c is the length of hypotenuse of a right angled triangle, while a and b are lengths of other two sides

Proof:

Consider the triangle ABC where $\angle$ B = $90^0$ as shown in the figure. Let’s draw BD line segment such that BD is perpendicular to side AC creating two right angled triangles BDA and BDC

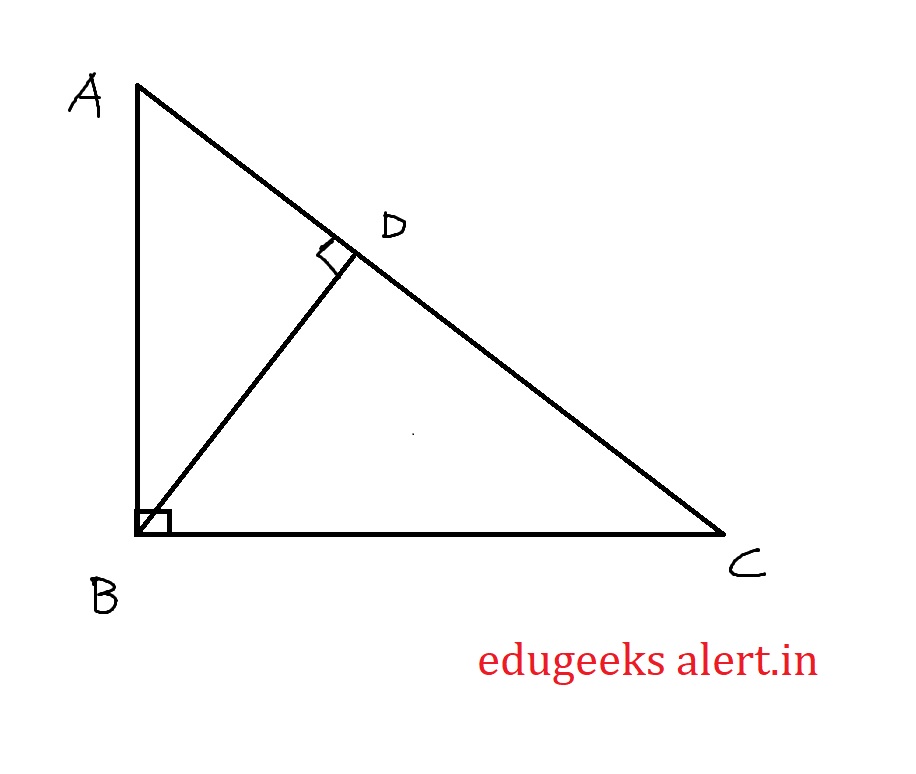
$$Let’s\ compare\ \triangle ABC\ with\ \triangle\ ABD$$

$$\angle BAC = \angle BAD$$

$$\angle ABC = \angle ADB = 90^0$$

Therefore by Angle-Angle axiom we can say that $\triangle$ ABC $\sim$ $\triangle$ ADB

$$\triangle ABC \sim \triangle ADB$$

$$\frac{AB}{AD}=\frac{AC}{AB}$$

$$AB^2 = AC AD ————(1)$$

Let’s compare \triangle ABC with $\triangle$ BDC

$$\angle BCA = \angle BCD$$

$$\angle ABC = \angle BDC = 90^0$$

Therefore by Angle-Angle axiom we can say that $\triangle$ ABC $\sim$ $\triangle$ BDC

$$\triangle ABC \sim \triangle BDC$$

$$\frac{BC}{DC}=\frac{AC}{BC}$$

$$BC^2 = DC AC ————(2)$$

From (1) and (2), Add (1) and (2)

$$AB^2 + BC^2 = AC AD + DC AC$$

$$AB^2 + BC^2 = AC ( AD + AC)$$

From the diagram we can see that AC = AD + AC

$$AB ^2 + BC^2 = AC ^2$$

Hence proved that in a right angled triangle square of length of hypotenuse is equal to the sum of squares of the lengths of other two sides.

5 - triangle

5.1 - Area of triangle proof

There are many formulae for the area of triangle, in this article we would like to prove the following formula of area of triangle. which is more commonly used in mathematics.

$1)\Delta = \frac{1}{2} base * height$ where base is one side of the triangle and height is the altitude on the considered side from the opposite vertex.

1) Proof of $\Delta\ = 1/2\ base * height$

Proof:

Let’s prove the formula using normal geometry. For that let’s consider a paralellogram ABCD as shown in the figure. As we can see in the diagram there is a triangle ABC in paralelllogram ABCD. since $\triangle ABC$ and $\triangle CDA$ have equal lenghts of sides both the triangles, that means both triangles are congruent, which means areas of $\triangle ABC$ and $\triangle CDA$ must be equal. that means area of paralellogram is twice the area of $\triangle ABC$ or $\triangle ADC$.

therefore area of $\triangle$ ABC = $\frac{1}{2}$ area of ABCD

Let’s not use the area of paralellogram formula blindly instead let’s understand how that formula is built. In order to find the area of paralellogram let’s draw DE and CF line segments perpendicular the side AB as shown below.

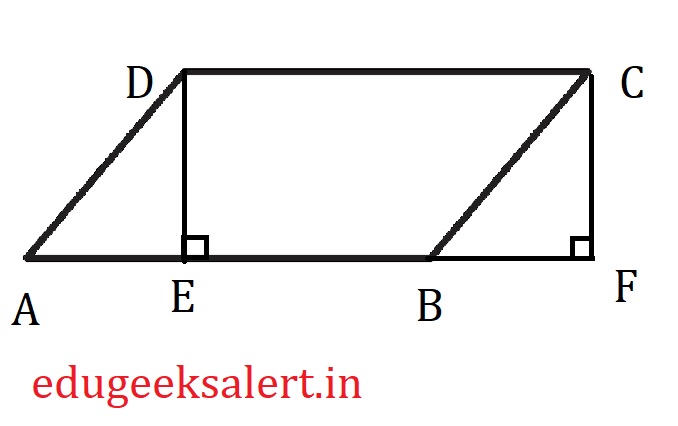
Now look at the diagram we have produced two triangles $\triangle$ ADE and $\triangle$ BCF, let’s prove that these two triangles are congruent.

$$In\ \triangle\ ADE\ and\ \triangle\ BCF$$

since AD and BC are opposite sides of paralellogram $$AD=BC$$

since AD $\parallel$ BC and AF is transversal corresponding angles must be equal, $$\angle DAE= \angle CBF$$

since $\angle DEA$= $\angle CFB$= $90^0$ and $\angle DAE= \angle CBF$ then $$\angle ADE=\angle BCF$$

by Angle Side Angle axiom $\triangle ADE$ and $\triangle BCF$ are congruent. By this we can say that:

$$area\ of\ paralellogram\ ABCD = area\ of\ rectangle\ EFCD$$

therefore, $$area\ of\ paralellogram\ ABCD = length * breadth$$

from the diagram we can understand that length of rectangle EFCD is base of $\Delta$ ABC and breadth of rectangle EFCD is altitude(height) of $\Delta$ ABC

therefore area of triangle ABC = $\frac{1}{2}$ area of paralellogram ABCD = $\frac{1}{2} base * height$

6 - Trigonometry

6.1 - Trigonometric Identities

1) $sin^2$ x + $cos^2$ x = 1

proof:

To prove this identity let us use pythagoras theorem. consider a right angled triangle as shown in the figure. It is a triangle ABC with right angle at the vertex B and angle x at vertex C.

According to pythagoras theorem we can write

$AB^2$ + $BC^2$ = $AC^2$

Divide with $AC^2$ on both sides.

$\frac{AB^2+BC^2}{AC^2}$ = 1

$\frac{AB^2}{AC^2}$ + $\frac{BC^2}{AC^2}$ = 1

by definition sin x = $\frac{opposite\ side\ to \ angle\ x}{hypotenuse}$ = $\frac{AB}{AC}$ and cos x = $\frac{adjacent \ side \ to\ angle \ x}{hypotenuse}$ = $\frac{CB}{AC}$

Therefore $sin^2$ x + $cos^2$ x = 1

I) Practice problems

1. If sin x = $\frac{4}{5}$ find the value of cos x provided x is acute angle.
2. find the value of $sin^2$ $50^0$ + $sin^2$ $40^0$
3. find th value of $sin^2$ $18^0$ + $sin^2$ $72^0$ + $sin^2$ $108^0$ + $sin^2$ $162^0$

Solutions at the end of the article.

2) $sec^2$ x - $tan^2$ x =1

proof:

To prove this identity let us use pythagoras theorem. consider a right angled triangle as shown in the figure. It is a triangle ABC with right angle at the vertex B and angle x at vertex C.

According to pythagoras theorem we can write

$AB^2$ + $BC^2$ = $AC^2$

Divide with $BC^2$ on both sides, so that we can get tan x and sec x functions in the equation.

$\frac{AB^2}{BC^2}$ + 1 = $\frac{AC^2}{BC^2}$

by definition tan x = $\frac{opposite\ side\ to\ angle\ x}{adjacent\ side\ to\ angle\ x}$ = $\frac{AB}{BC}$ and sec x = $\frac{hypotenuse}{adjacent\ side\ to\ angle\ x}$ = $\frac{AC}{BC}$

Therefore $tan^2$ x + 1 = $sec^2$ x

II) solve the following problem

1. If sec A + tan A = 4, find the value of sin A.
2. Prove that $\frac{tan\ A+sec\ A -1}{tan\ A-sec\ A +1}$ = $\frac{1+sin\ A}{cos\ A}$

Solutions at the end of the article.

3) $cosec^2$ x - $cot^2$ x =1

proof:

To prove this identity let us use pythagoras theorem. consider a right angled triangle as shown in the figure. It is a triangle ABC with right angle at the vertex B and angle x at vertex C.

According to pythagoras theorem we can write

$AB^2$ + $BC^2$ = $AC^2$

Divide with $AB^2$ on both sides, so that we can get tan x and sec x functions in the equation.

$\frac{BC^2}{AB^2}$ + 1 = $\frac{BC^2}{AC^2}$

by definition cot x = $\frac{adjacent\ side\ to\ angle\ x}{opposite\ side\ to\ angle\ x}$ = $\frac{BC}{AB}$ and cosec x = $\frac{hypotenuse}{opposite\ side\ to\ angle\ x}$ = $\frac{BC}{AC}$

Therefore $cosec^2$ x - $cot^2$ x =1

III) solve the following

1. find the value of (sin x + cosec x) $^2$ + (cos x + sex x) $^2$ - (tan x + cot x) $^2$
2. If Cosex A + Cot A = $\frac{2}{3}$ find the value of Sin A

Solutions at the end of the article.

Solutions

I)

1. ans= $\frac{3}{5}$

sol: Given Sin x = $\frac{4}{5}$

using the identity of trigonometry

$sin^2$ x + $cos^2$ x = 1

$\frac{4^2}{5^2}$ + $cos^2$ x = 1

$cos^2$ x = $\frac{9}{25}$

cos x = + $\frac{3}{5}$ or - $\frac{3}{5}$

2. ans= 1

sol:

$sin^2$ $50^0$ + $sin^2$ $40^0$

= $sin^2$ $50^0$ + $sin^2$ $(90^0-50^0)$

= $sin^2$ $50^0$ + $cos^2$ $50^0$

use the identity of trigonometry $sin^2$ x + $cos^2$ x = 1

= 1

3. ans= 2

sol:

$sin^2$ $18^0$ + $sin^2$ $72^0$ + $sin^2$ $108^0$ + $sin^2$ $162^0$

= $sin^2$ $18^0$ + $sin^2$ $72^0$ + $sin^2$ $(90^0+18^0)$ + $sin^2$ $(90^0+72^0)$

= $sin^2$ $18^0$ + $sin^2$ $72^0$ + $cos^2$ $18^0$ + $cos^2$ $72^0$

= ($sin^2$ $18^0$ + $cos^2$ $18^0$ ) + ( $sin^2$ $72^0$ + $cos^2$ $72^0$ )

use the identity of trigonometry $sin^2$ x + $cos^2$ x = 1

= 2

II)

1. Ans= $\frac{15}{17}$

Sol:

given sec A+tan A=4

let’s use the trigonometric identity

$sec^2$ x - $tan^2$ x =1

use the algebraic equation $a^2-b^2$=(a+b)(a-b)

(sec A + tan A)(Sec A - tan A) =1

4*(Sec A - tan A) =1

Sec A - tan A = $\frac{1}{4}$

adding the two equations

(Sec A + tan A)+(Sec A - tan A)= 4+ $\frac{1}{4}$

sec A = $\frac{17}{8}$

similarly subtracting the two equations

(Sec A + tan A)-(Sec A - tan A) = 4- $\frac{1}{4}$

tan A = $\frac{15}{8}$

on divinding tan A with sec A we get sin A

sin A = $\frac{15}{8}$ * $\frac{8}{17}$

sin A = $\frac{15}{17}$

Sol:

Consider LHS

$\frac{tan\ A+sec\ A -1}{tan\ A-sec\ A +1}$

multiply and divide the fraction with $tan\ A+sec\ A +1$

= $\frac{ [ (tan\ A+sec\ A) -1 ][(tan\ A+sec\ A) +1 ]}{[(tan\ A+1)-sec\ A][(tan\ A+1) +sec\ A]}$

= $\frac{ (tan\ A+sec\ A)^2 -1}{(tan\ A+1)^2-sec^2\ A}$

= $\frac{tan^2\ A+ sec^2\ A+2tan\ A sec\ A -1}{tan^2\ A+2tan\ A+1-sec^2\ A}$

use the trigonometric identity $sec^2$ x - $tan^2$ x =1 which can also be written as $sec^2$ x -1= $tan^2$ x

= $\frac{2tan^2\ A +2tan\ A sec\ A}{2tan\ A+1-1}$

= tan A + sec A

= $\frac{sin\ A}{cos\ A}$ + $\frac{1}{cos\ A}$

= $\frac{1+sin\ A}{cos\ A}$

III)

1. ans = 5 Sol:

(sin x + cosec x) $^2$ + (cos x + sex x) $^2$ - (tan x + cot x) $^2$

= $sin^2$ x + $cosec^2$ x + 2+ $cos^2$ x+ $sec^2$ x+ 2 - $tan^2$ x - $cot^2$ x-2

= ( $sin^2$ x + $cos^2$ x)+( $cosec^2$ x- $cot^2$ x) + ( $sec^2$ x- $tan^2$ x) + 2

= 5

2. ans= $\frac{3}{13}$

Sol:

Cosex A + Cot A = $\frac{2}{3}$

let’s use the trigonometric identity

$cosec^2$ x - $cot^2$ x =1

use the algebraic equation $a^2-b^2$=(a+b)(a-b)

(Cosex A + Cot A)(Cosex A - Cot A)=1

$\frac{2}{3}$ (Cosex A - Cot A)=1

(Cosex A - Cot A)= $\frac{3}{2}$

add both the equations

(Cosex A + Cot A)+(Cosex A - Cot A)= $\frac{2}{3}$ + $\frac{3}{2}$

cosec A = $\frac{13}{3}$

sin A = $\frac{3}{13}$

6.2 - Trigonometric Identities (problem solving)

1) If cos 2A = $tan^2$ B then find the value of $tan^2$ A in terms of B.

Sol:

Given, cos 2A = $tan^2$ B

Use multiple angle formula of cos, i.e. cos 2A = $\frac{1- tan^2\ A}{1+ tan^2\ A}$

$\frac{1- tan^2\ A}{1+ tan^2\ A}$ = $tan^2$ B

1- $tan^2$ A = $tan^2$ B (1+ $tan^2$ A)

1- $tan^2$ A = $tan^2$ B + $tan^2$ B $tan^2$ A

1- $tan^2$ B = $tan^2$ A + $tan^2$ B $tan^2$ A

1- $tan^2$ B = $tan^2$ A(1- $tan^2$ B)

$\frac{1- tan^2\ B}{1+ tan^2\ B}$ = $tan^2$ A

Again use the formula cos 2A = $\frac{1- tan^2\ A}{1+ tan^2\ A}$

cos 2B = $tan^2$ A

Therefore $tan^2$ A = cos 2B

2) If a cos A - b sin A = c then find the value of a sin A + b cos A

Sol:

Given, a cos A - b sin A = c

Squaring on both sides

$(a cos A - b sin A)^2$ = $c^2$

$a^2\ cos^2$ A + $b^2\ sin^2$ A -2ab sin A cos A = $c^2$

$a^2\ (1-sin^2$ A) + $b^2\ (1-sin^2$ A) -2ab sin A cos A = $c^2$

$a^2$ - $a^2\ sin^2$ A + $b^2$ - $b^2\ sin^2$ A -2ab sin A cos A = $c^2$

$a^2$ + $b^2$ - ( $a^2\ sin^2$ A + $b^2\ sin^2$ A + 2ab sin A cos A) = $c^2$

(a sin A + b cos A $)^2$ = $a^2$ + $b^2$ - $c^2$

a sin A + b cos A = $\pm \sqrt{a^2 + b^2 - c^2}$

3) If sin A + cosec A = 2 then find the value of sin $^20$ A + cosec $^20$ A

Sol:

sin A + cosec A = 2

sin A + $\frac{1}{sin\ A}$ = 2

Sin $^2$ A + 1 = 2 sin A

Sin $^2$ A + 1 - 2 sin A = 0

(sin A - 1 $)^2$ = 0

Sin A = 1

So cosec A = 1

sin $^20$ A + cosec $^20$ A =1+1

sin $^20$ A + cosec $^20$ A = 2

4) If sin A + sin $^2$ A + sin $^3$ A = 1 find the value of cos $^6$ A - 4cos $^4$ A + 8cos $^2$

Sol:

Given, sin A + sin $^2$ A + sin $^3$ A = 1

sin A + sin $^3$ A = 1- sin $^2$ A

sin A + sin $^3$ A = cos $^2$ A

Square on both sides

( sin A + sin $^3$ A $)^2$ = cos $^4$ A

sin $^2$ A + 2sin $^4$ A + sin $^6$ A = cos $^4$ A

1-cos $^2$ A + 2(1-cos $^2$ A $)^2$ + (1-cos $^2$ A $)^3$ = cos $^4$ A

1-cos$^2$ A + 2-4cos $^2$ A + 2cos $^4$ A + 1- 3cos $^2$ A + 3cos $^4$ A - cos $^6$ A = cos $^4$ A

4 - cos $^6$ A + 4cos $^4$ A - 8cos $^2$ = 0

Therefore cos $^6$ A - 4cos $^4$ A + 8cos $^2$= 0

5) if sin A + cos A = m and sin $^3$ A + cos $^3$ A = n, then prove that m$^3$ -3m+2n=0

sol:

Given,

sin A + cos A = m and sin $^3$ A + cos $^3$ A = n

Consider the second equation

sin $^3$ A + cos $^3$ A = n

Use the algebraic formula a $^3$ A + b $^3$ A = (a+b)( a $^2$ - ab + b $^2$ )

(sin A + cos A)( sin $^2$ A - sin A cos A + cos $^2$ A) = n

But it is given that sin A + cos A = m and we know that sin $^2$ A + cos $^2$ A = 1

m(1 - sin A cos A) = n ————–(1)

Now let’s consider the given equation sin A + cos A = m and lets square on both sides of the equation

(sin A + cos A $)^2$ = m $^2$

sin $^2$ A + 2sin A cos A + cos $^2$ A = m $^2$

we know that sin $^2$ A + cos $^2$ A = 1

1 + 2sin A cos A = m $^2$ sin A cos A = $\frac{m^2 -1}{2}$ ————(2)

Now from (1) and (2)

m(1 - $\frac{m^2 -1}{2}$) = n

2m - m $^3$ +m = 2n

m$^3$ -3m+2n=0

6.3 - Trigonometric ratios of multiple of Angle-2A

If A an angle, then its integral multiples 2A, 3A, 4A….. are called multiple angles of A and the multiple angles of A

Trigonometric ratios of Multiple angles of A Formulae

1. Sin 2A = 2Sin A cos A

2. cos 2A = $cos^2$ A - $sin^2$ A = 2 $cos^2$ A-1 = 1- $sin^2$ A

3. tan 2A = $\frac{2tan\ A}{1-tan^2\ A}$

4. cot 2A = $\frac{cot^2\ A-1}{2cot\ A}$

5. Sin 2A = $\frac{2tan\ A}{1+tan^2\ A}$

6. cos 2A = $\frac{1-tan^2\ A}{1+tan^2\ A}$

1) Sin 2A = 2Sin A cos A

Proof:

We have a compound angle formula:

Sin(A+B)= sin A cos B + cos A sin B

If A=B

Sin 2A = sin A cos A + cos A sin A

Sin 2A = 2sin A cos A

2) cos 2A = $cos^2$ A - $sin^2$ A = 2$cos^2$ A-1 = 1- $sin^2$ A

Proof:

i) We have a compound angle formula:

Cos(A+B)= Cos A cos B- Sin A Sin B

If A= B

Cos 2A = $cos^2$ A - $sin^2$ A

ii) Using the trigonometric identity $cos^2$ A + $sin^2$ A =1 in Cos 2A = $cos^2$ A - $sin^2$ A

Cos 2A = (1-$sin^2$ A)-$sin^2$ A

Cos 2A = 1-2$sin^2$ A

iii) Similarly Using the trigonometric identity $cos^2$ A + $sin^2$ A =1 in Cos 2A = $cos^2$ A - $sin^2$ A

Cos 2A = $cos^2$ A - $sin^2$ A

Cos 2A = $cos^2$ A - (1-$cos^2$ A)

Cos 2A = 2 $cos^2$ A -1

Therefore cos 2A = $cos^2$ A - $sin^2$ A = 2$cos^2$ A-1 = 1- $sin^2$ A

3) tan 2A = $\frac{2tan\ A}{1-tan^2\ A}$

Proof:

tan 2A = $\frac{sin\ 2A}{cos\ 2A}$

Using the multiple angle formulae Sin 2A=2Sin A cos A and cos 2A = $cos^2$ A - $sin^2$ A

tan 2A = $\frac{2Sin\ A cos\ A}{cos^2\ A - sin^2\ A }$

Divide $cos^2$ A on both numerator and denominator.

tan 2A = $\frac{\frac{2Sin\ A cos\ A}{cos^2\ A}}{\frac{cos^2\ A - sin^2\ A}{cos^2\ A }}$

tan 2A = $\frac{2tan\ A}{1-tan^2\ A}$

4) cot 2A = $\frac{cot^2\ A-1}{2cot\ A}$

Proof:

Cot 2A = $\frac{1}{tan\ 2A}$

Using tan 2A = $\frac{2tan\ A}{1-tan^2\ A}$ formula

Cot 2A = $\frac{1-tan^2\ A}{2tan\ A}$

= $\frac{1-\frac{1}{cot^2\ A}}{2\frac{1}{cot\ A}}$

cot 2A = $\frac{cot^2\ A-1}{2cot\ A}$

5) Sin 2A = $\frac{2tan\ A}{1+tan^2\ A}$

Proof:*

We have a trigonometric multiple angle formula:

Sin 2A=2Sin A cos A

Use trigonometric identity $cos^2$ A + $sin^2$ A =1

Sin 2A = $\frac{2Sin\ A cos\ A}{cos^2\ A + sin^2\ A}$

Divide with $cos^2$ A on numerator and denominator

Sin 2A = $\frac{\frac{2Sin\ A cos\ A}{cos^2\ A}}{\frac{cos^2\ A + sin^2\ A}{cos^2\ A} }$

Sin 2A = $\frac{2tan\ A}{1+tan^2\ A}$

6) cos 2A = $\frac{1-tan^2\ A}{1+tan^2\ A}$

Proof:

We have a trigonometric multiple angle formula:

cos 2A = $cos^2$ A - $sin^2$ A

Use trigonometric identity $cos^2$ A + $sin^2$ A =1

Cos 2A = $\frac{cos^2\ A-sin^2\ A}{cos^2\ A+sin^2\ A}$

Divide with $cos^2$ A on numerator and denominator

Cos 2A = $\frac{\frac{cos^2\ A-sin^2\ A}{cos^2\ A}}{\frac{cos^2\ A+sin^2\ A}{cos^\ A}}$

Cos 2A = $\frac{1-tan^2\ A}{1+tan^2\ A}$

6.4 - Trigonometric ratios of multiple of Angle-3A

Page contents:

proofs of sin 3A, cos 3A, tan 3A, cot 3A

Formulae:

1. Sin 3A = 3Sin A-4 $sin^3$ A
2. cos 3A = 4 $cos^3$ A - 3cos A
3. tan 3A = $\frac{3tan\ A-tan^3\ A}{1-3tan^2\ A}$
4. cot 3A = $\frac{3cot\ A-cot^3\ A}{1-3cot^\ A}$

1) Sin 3A = 3Sin A-4 $sin^3$ A

Proof:

Sin 3A = sin(A +2A)

use compund angle formula of sine function, i.e. Sin(A+B)= sinA cosB + cosA sinB

Sin 3A = sin 2A cos A + cos 2A sin A

use Sin 2A = 2sin A cos A; Cos 2A = 1-2 $sin^2 A$

Sin 3A = 2sin A $cos^2$ A + (1-2 $sin^2 A$) sin A

using the trigonometric identity $sin^2$ A + $cos^2$ A =1

sin 3A = 2sin A(1- $sin^2$ A) + sin A - 2 $sin^3 A$

Sin 3A = 3Sin A-4 $sin^3$ A

2) Cos 3A = 4 $cos^3$ A - 3cos A

Proof:

cos 3A = cos(A+2A)

use compund angle formula of sine function, i.e. cos(A+B)= cosA cosB + sinA sinB

cos(A+2A)= cosA cos2A + sinA sin 2A

use Sin 2A = 2sin A cos A; Cos 2A = 2 $cos^2 A$-1

cos 3A = cos A(2 $cos^2 A$-1) + sin A 2sin Acos A

cos 3A = 2 $cos^3 A$ -cos A +2 $sin^2$ A cos A

using the trigonometric identity $sin^2$ A + $cos^2$ A =1

cos 3A = 2 $cos^3 A$ -cos A +2(1- $cos^2$ A) cos A

Cos 3A = 4 $cos^3$ A - 3cos A

3) tan 3A = $\frac{3tan\ A-tan^3\ A}{1-3tan^2\ A}$

Proof:

tan 3A = tan(A+2A)

use compund angle formula of sine function, i.e. tan(A+B) = $\frac{tan\ A+tan\ B}{1-tan\ Atan\ B}$

tan 3A = $\frac{tan\ A+tan\ 2A}{1-tan\ Atan\ 2A}$

use the formula tan 2A = $\frac{2tan\ A}{1-tan^2\ A}$

tan 3A = $\frac{tan\ A+\frac{2tan\ A}{1-tan^2\ A}}{1-tan\ A\frac{2tan\ A}{1-tan^2\ A}}$

tan 3A = $\frac{3tan\ A-tan^3\ A}{1-3tan^2\ A}$

4) cot 3A = $\frac{3cot\ A-cot^3\ A}{1-3cot^\ A}$

Proof:

cot 3A = cot(A+2A)

use compund angle formula of sine function, i.e. cot(A+B) = $\frac{cot\ A cot\ B-1}{cot\ A+cot\ B}$

cot 3A = $\frac{cot\ A cot\ 2A-1}{cot\ A+cot\ 2A}$

use the formula cot 2A = $\frac{cot^2\ A-1}{2cot\ A}$

cot 3A = $\frac{cot\ A \frac{cot^2\ A-1}{2cot\ A}-1}{cot\ A+\frac{cot^2\ A-1}{2cot\ A}}$

cot 3A = $\frac{3cot\ A-cot^3\ A}{1-3cot^\ A}$

6.5 -

6.6 - Trigonometric transformations from sum( or difference) to product and vice-versa

Formulae

sum into product transformations:

2sin A cos B = sin(A+B) + sin(A-B)

2cos A sin B = sin(A+B) - sin(A-B)

2cos A cos B = cos(A-B) + cos(A+B)

2sin A sin B = cos(A-B) - cos(A+B)

product into sum transformations:

sin C + sin D = 2sin( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ )

sin C - sin D = 2cos( $\frac{C+D}{2}$ ) sin( $\frac{C-D}{2}$ )

cos C + cos D = 2cos( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ )

cos C - cos D = -2sin( $\frac{C+D}{2}$ ) sin( $\frac{C-D}{2}$ )

Proofs

2sin A cos B = sin(A+B) + sin(A-B)

Proof:

consider Right hand sideo of the statement

sin(A+B) + sin(A-B)

use the coumpund angle formulae i.e. sin(A+B) = sin A cos B + cos A sin B and sin(A-B) = sin A cos B - cos A sin B

sin(A+B) + sin(A-B) = (sin A cos B + cos A sin B) + (sin A cos B - cos A sin B)

sin(A+B) + sin(A-B) =2sin A cos B

hence 2sin A cos B = sin(A+B) + sin(A-B)

sin C + sin D = 2sin( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ )

Proof:

consider Right hand sideo of the statement

2sin( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ )

this looks liks the previous proof statement i.e 2sin A cos B = sin(A+B) + sin(A-B) where A = $\frac{C+D}{2}$ and B = $\frac{C-D}{2}$

2sin( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ ) = sin( $\frac{C+D}{2}$ + $\frac{C-D}{2}$ ) cos ( $\frac{C+D}{2}$ - $\frac{C-D}{2}$ )

2sin( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ ) = sin C + sin D

hence sin C + sin D = 2sin( $\frac{C+D}{2}$ ) cos( $\frac{C-D}{2}$ )

similalry rest of the proofs can be done

2cos A sin B = sin(A+B) - sin(A-B)

Proof:

consider Right hand sideo of the statement

sin(A+B) - sin(A-B)

use the coumpund angle formulae i.e. sin(A+B) = sin A cos B + cos A sin B and sin(A-B) = sin A cos B - cos A sin B

sin(A+B) sin(A-B) = (sin A cos B + cos A sin B) (sin A cos B - cos A sin B)

sin(A+B) + sin(A-B) = 2cos A sin B

hence 2cos A sin B = sin(A+B) - sin(A-B)

2cos A cos B = cos(A-B) + cos(A+B)

proof:

consider Right hand sideo of the statement

cos(A-B) + cos(A+B)

use the coumpund angle formulae i.e. cos(A+B) = cos A cos B - sin A sin B and cos(A-B) = cos A cos B + sin A sin B

cos(A-B) + cos(A+B) = (cos A cos B - sin A sin B) + (cos A cos B - sin A sin B)

cos(A-B) + cos(A+B) = 2cos A cos B

hence 2cos A cos B = cos(A-B) + cos(A+B)

2sin A sin B = cos(A-B) - cos(A+B)

proof:

consider Right hand sideo of the statement

cos(A-B) - cos(A+B)

use the coumpund angle formulae i.e. cos(A+B) = cos A cos B - sin A sin B and cos(A-B) = cos A cos B + sin A sin B

cos(A-B) - cos(A+B) = (cos A cos B - sin A sin B) - (cos A cos B - sin A sin B)

cos(A-B) - cos(A+B) = 2sin A sin B

hence 2sin A sin B = cos(A-B) - cos(A+B)

7 - Trigonometric Properties of triangle

7.1 - cos rules or Laws of cos

Cos rule or law of cos states that in A $\triangle$ ABC a, b and c are lengths of sides BC CA and AB. Then

$$a^2=b^2+c^2-2bc \ Cos \ A$$

$$b^2=a^2+c^2-2ac\ Cos\ B$$

$$c^2=a^2+b^2-2ab\ Cos\ C$$

$$Or$$

$$cos\ B= \frac{a^2+c^2-b^2}{2ac}$$

$$cos\ C= \frac{b^2+a^2-c^2}{2ba}$$

$$cos\ A= \frac{b^2+c^2-a^2}{2bc}$$

It seems like a different form of Pythagoras theorem for every triangle doesn’t it?

Proof:

Let’s consider a $\triangle$ ABC as shown in the figure with a, b and c being the lengths of the sides BC, CA and AB. we can represent the triangle vectorically as shown in the diagram. That means $\vec{AB}$, $\vec{BC}$ and $\vec{AC}$ are forming the triangle so we can understand that | $\vec{AB}$ | = c, | $\vec{BC}$ | = a and | $\vec{AC}$ | = b.

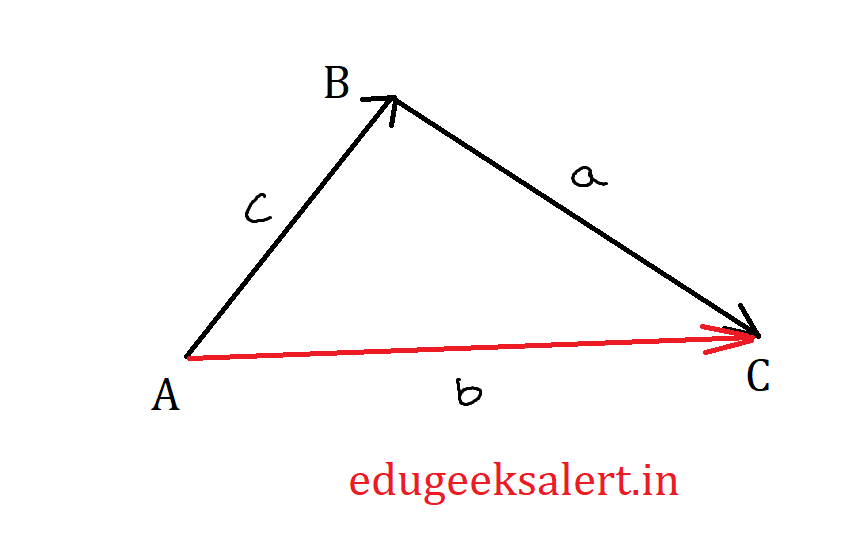
From the triangle we can write that

$$\vec{AC}=\vec{AB}+\vec{BC}$$

Apply mod on both sides

$$| \vec{AC} |=| \vec{AB} + \vec{BC} |$$

$$ b = | \vec{AB} + \vec{BC} |$$

From vectors we have $| \vec{x} + \vec{y} | = \sqrt {x^2+y^2+2xy\ cos(\vec{x},\vec{y})}$

To find the angle between $\vec{AB}$ and $\vec{BC}$ lets extend the $\vec{AB}$ so that both vector tails meet. Let $\alpha$ be the angle between those two vectors.

(note: we extended the vector to find the angle between two vectors by not considering B as angle, because angle between two vectors is angle made by vectors when both heads meet or tails meet but not one tail and one head)

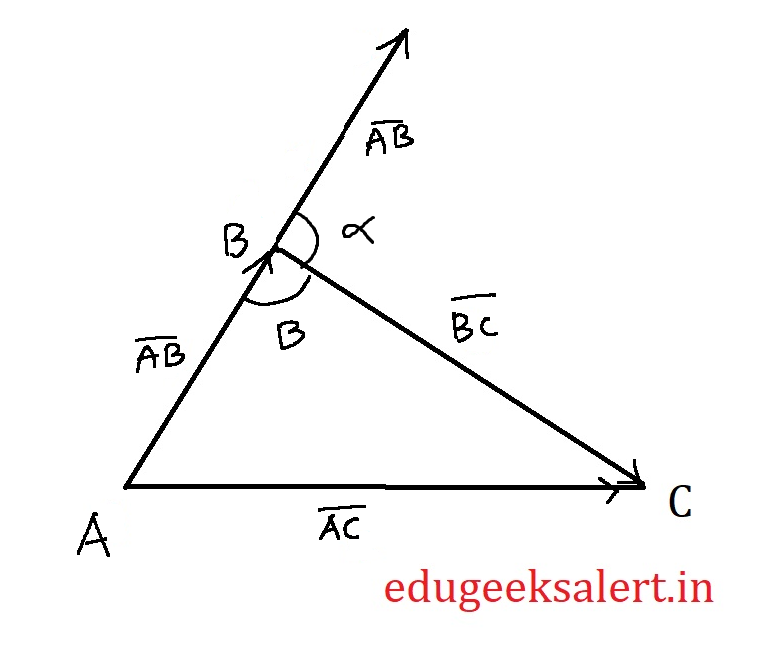
From the above figure we can find $\alpha$

$$\alpha + B=180^0$$

$$\alpha =180^0 - B $$

Therefore,

$$ b = | \vec{AB} + \vec{BC} |$$

$$ b =\sqrt{ | \vec{AB}|^2 +| \vec{BC} |^2 +2 | \vec{AB} | |\vec{BC}| cos(\vec{AB} , \vec{BC})}$$

$$ b =\sqrt{ c^2 + a^2 +2 ca\ cos(\alpha)}$$

$$ b =\sqrt{ c^2 + a^2 +2 ca\ cos(180^0 - B)}$$

$$ b =\sqrt{ c^2 + a^2 -2 ca\ cos\ B}$$

$$b^2=a^2+c^2-2ac\ Cos\ B$$

Hence proved.

Now we can extend this proof by simplification and we can write

$$cos\ B= \frac{a^2+c^2-b^2}{2ac}$$

Similarly we can do the same for the other two angles and we can prove the other two equations of cos rule

7.2 - Sine rule or Laws of sine

Statement: In a $\triangle$ ABC with a, b and c are the lengths of sides BC, CA and AB respectively then

$$\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}= 2R$$

Where R is the circum radius of the $\triangle$ ABC.

Therefore, $$a= 2R\ Sin\ A, b= 2R\ sin\ B, c= 2R\ sin\ C$$

Proof: Let’s consider the $\triangle$ ABC as shown in the figure circumscribed. O is the circum centre.

We know that a, b and c are lengths of sides of $\triangle$ ABC and R is the circum radius.

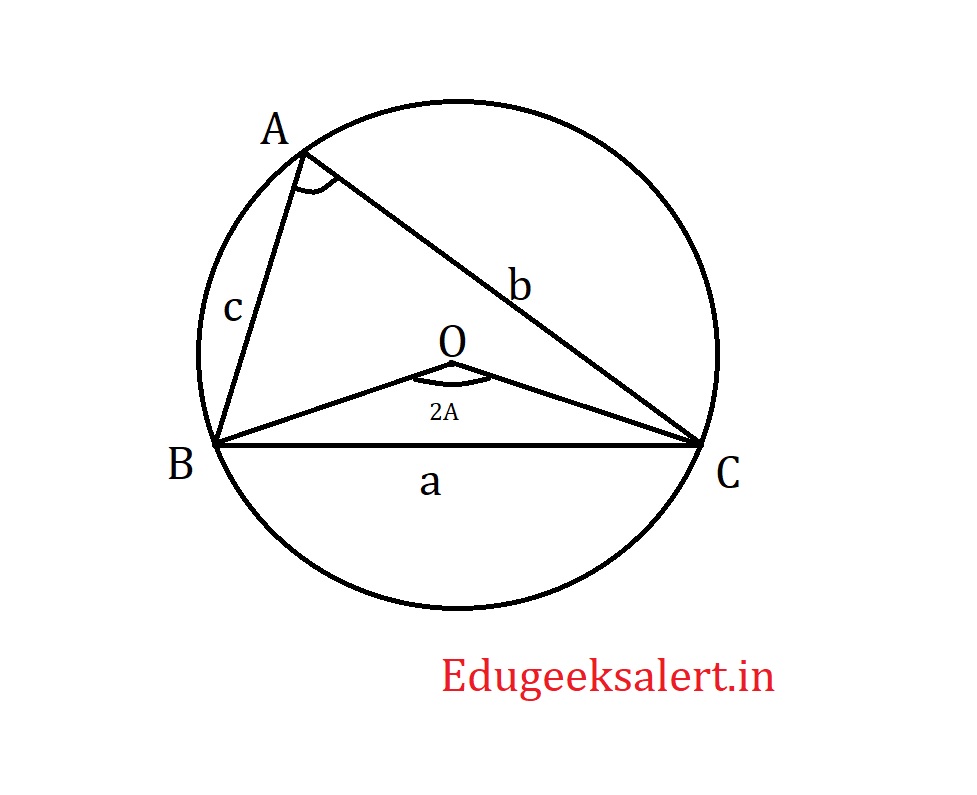
From the diagram we can see that BC is the chord of the circle. From circle properties we know that

$$\angle BOC = 2A$$

Let’s draw altitude to OM in $\triangle$OBC perpendicular to side BC. As OB and OC are also radii of the circle we can understand that $\triangle$OBC is an isosceles triangle. In an isosceles triangle altitude and median coincides. Therefore OM is not just altitude but also median. Therefore BM =$\frac{a}{2}$

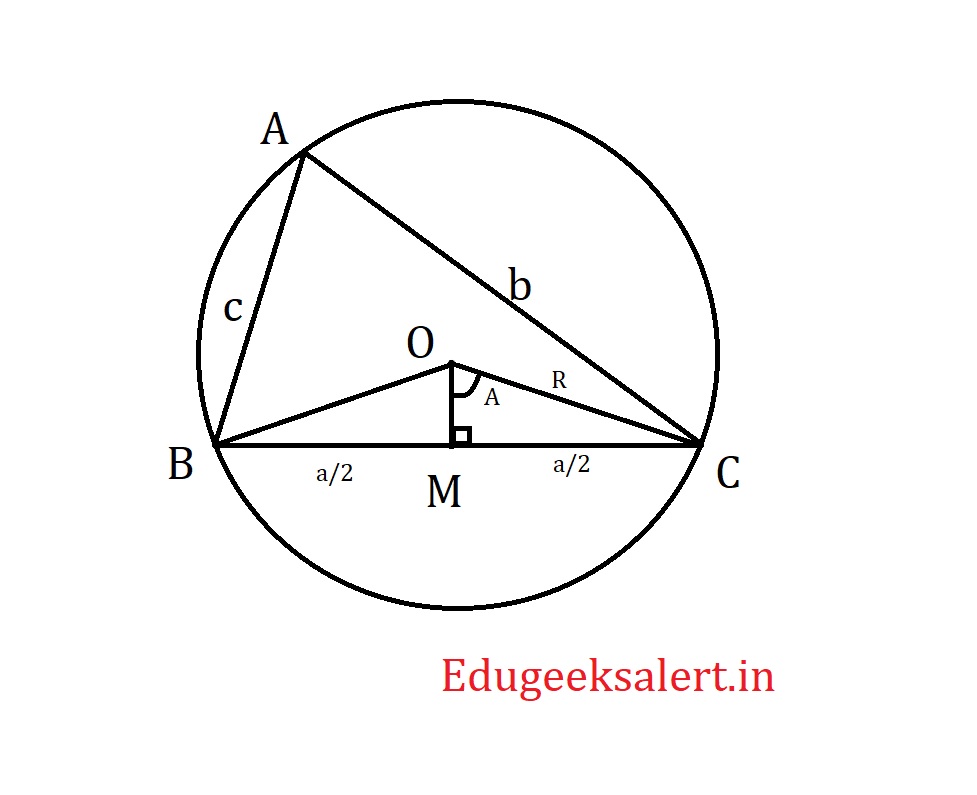
Now let’s consider $\triangle$ OMB, since OBC is isosceles OM bisects $\angle$ BOC. And $\angle$ OMB =$90^0$

$$sin \ \angle BOM = \frac{MB}{OB}$$

$$sin \ A= \frac{a}{2R}$$

$$a=2R\ sin\ A$$

Similarly we can prove that c = 2R sin C and b= 2R sin B.

And we can write

$$\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}= 2R$$